What is the difference between you and me? Not the breakfast we ate yesterday that is part of us today and will be gone tomorrow. Even though we may have eaten the same foods, you are still the unique you and quite different from me.

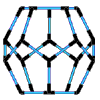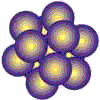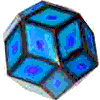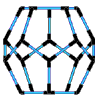
     Think of the carbon molecule in a hexagonal pattern known as graphite, or in a tetrahedronal pattern known as diamond or as a somewhat spherical icosahedronal pattern known as C 60 carbon (Buckminsterfullerene). All are the same carbon molecule with different properties according to geometric patterns and constraints.

     The difference between you and me and the carbon molecules we all share, is pattern integrity or simply stated, geometry. I find geometry to be an exhilarating and fascinating study. However, most who have taken a course or two in Euclidean geometry (including me) come away with, at worst, a fear of math, and if you are like most people, a vague understanding of the difficult axiomatic process that seems to have little practical application.

     No, it wasn't the high school geometry classes or the course work leading to a degree in engineering that excited me about geometry. It was when I came across the work of Buckminster Fuller that I became excited about the inter-transforming properties of geometry and the applications to be found every where, in and between everything.

     Bucky starts with a comprehensive view of nature that requires modeling reality. No non-dimensional (imaginary) points or lines and planes extending into infinity without thickness or volume are allowed. To be a point (a basic geometric point) requires volume and a minimal sized point must be a modelable Tetrahedron a four faced triangulated enclosure (3 or less faces does not enclose volume).

      I was amazed with the logic. To follow Bucky's work requires modeling in 3-dimensions. Seeing a picture of a tetrahedron falls short. Feeling the omni-triangulated strength of a tetrahedron you just made is an experience that registers in the mind as well as the body. This giving understanding to the hardest mineral in nature, the tetrahedronally patterned diamond.

      To feel the flexibility of a cube is just as amazing. A child looks around and observes cubic architecture and assumes that the cube is structural, but this is not so. The triangle is the only polygon to hold its shape and is basic to all structure. The structural triangles in our building are mostly hidden. Experiencing the strength of a triangle leads to an understanding that a omni-triangulated structures such as Epcots center, requires no inside walls or columns. Squared or rectangular building require internal columns or supports and are thus a much larger investment in materials, labor and costs.

     To prove this requires the axioms of mathematics, to understand and feel this truth requires only models that children can make from simple inexpensive materials.

      One focus of handsonmath.com is to continue develop a curriculum on modeling geometric forms that offer a basic understanding of the constraints of space, geometric inter transformations and systems structure. Concepts are revealed in closest packing spheres, great circles, strut outlines, paper shapes and tensegrity models. The inexpensive materials we use are small spheres , bamboo skewers, rubber tubing, paper, tape and fishing line. The tools we employ are scissors, hand held hole punchers, clippers, low temperature glue guns and a cribbage board. Our curriculum is designed to be understood with little training, we do offer seminars and workshops for groups, teachers and individuals, as well as online assistance and instruction via the Internet. The study of geometry should begin with experimentation, conceptualization, modeling and, finally, axiomatic proof.

By Charles Gronberg    

     If you are interested in learning how to build these geometric manipulatives, and you would like more information on how to join. Please proceed to the Membership  page to review the benefits and pricing.